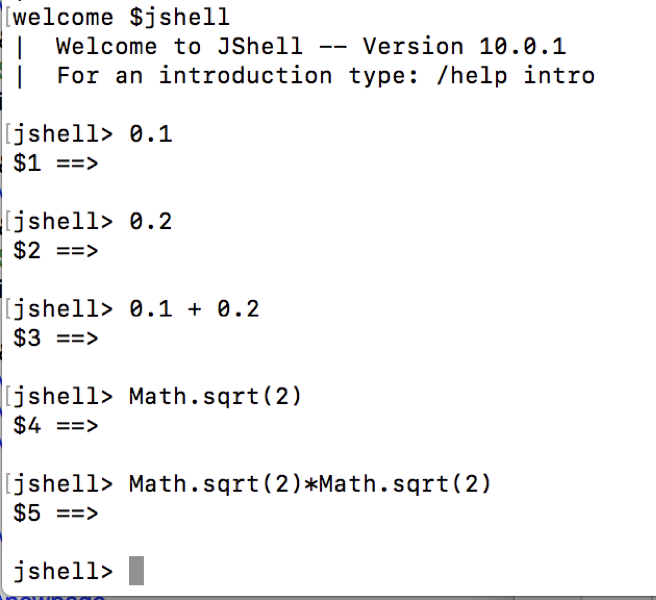
 Note: Java uses floating point, not
fixed width representation, but similar rounding errors appear in
both.
Note: Java uses floating point, not
fixed width representation, but similar rounding errors appear in
both.Definition For \(b\) an integer greater than \(1\), \(w\) a positive integer, \(w'\) a positive integer, and \(x\) a real number the base \(b\) fixed-width expansion of \(x\) with integer part width \(w\) and fractional part width \(w'\) is \((a_{w-1} \cdots a_1 a_0 . c_{1} \cdots c_{w'})_{b,w,w'}\) where \(a_0, a_1, \ldots, a_{w-1}, c_1, \ldots, c_{w'}\) are nonnegative integers less than \(b\) and \[x \geq \sum_{i=0}^{w-1} a_{i} b^{i} + \sum_{j=1}^{w'} c_{j} b^{-j} \hfill \textrm{\qquad and \qquad} \hfill x < \sum_{i=0}^{w-1} a_{i} b^{i} + \sum_{j=1}^{w'} c_{j} b^{-j} + b^{-w'}\]
| \(3.75\) in fixed-width binary, | |
| integer part width \(2\), | |
| fractional part width \(8\) | |
| \(0.1\) in fixed-width binary, | |
| integer part width \(2\), | |
| fractional part width \(8\) | |
 Note: Java uses floating point, not
fixed width representation, but similar rounding errors appear in
both.
Note: Java uses floating point, not
fixed width representation, but similar rounding errors appear in
both.