Monday October 11
Logical operators aka propositional
connectives
| Conjunction |
AND |
\(\land\) |
\land |
2 inputs |
Evaluates to \(T\) exactly when
both inputs are \(T\) |
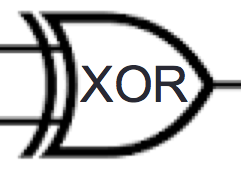
| Exclusive
or |
XOR |
\(\oplus\) |
\oplus |
2 inputs |
Evaluates to \(T\) exactly when exactly
one of inputs is \(T\) |
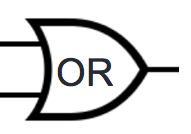
| Disjunction |
OR |
\(\lor\) |
\lor |
2 inputs |
Evaluates to \(T\) exactly when at least
one of inputs is \(T\) |
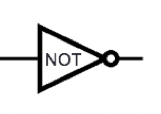
| Negation |
NOT |
\(\lnot\) |
\lnot |
1 input |
Evaluates to \(T\) exactly when its input is \(F\) |
Truth tables: Input-output tables where we use \(T\) for \(1\) and \(F\) for \(0\).
| Input |
Output |
|
|
Conjunction |
Exclusive
or |
Disjunction |
| \(p\) |
\(q\) |
\(p \land
q\) |
\(p \oplus q\) |
\(p
\lor q\) |
| \(T\) |
\(T\) |
\(T\) |
\(F\) |
\(T\) |
| \(T\) |
\(F\) |
\(F\) |
\(T\) |
\(T\) |
| \(F\) |
\(T\) |
\(F\) |
\(T\) |
\(T\) |
| \(F\) |
\(F\) |
\(F\) |
\(F\) |
\(F\) |
|
|
 |
 |
 |
| Input |
Output |
|
Negation |
| \(p\) |
\(\lnot
p\) |
| \(T\) |
\(F\) |
| \(F\) |
\(T\) |
|
 |
| Input |
Output |
| \(p\) |
\(q\) |
\(r\) |
|
\((p \land q)
\oplus (~ ( p \oplus q) \land r~)\) |
\((p \land q)
\vee (~ ( p \oplus q) \land r~)\) |
| \(T\) |
\(T\) |
\(T\) |
|
|
|
| \(T\) |
\(T\) |
\(F\) |
|
|
|
| \(T\) |
\(F\) |
\(T\) |
|
|
|
| \(T\) |
\(F\) |
\(F\) |
|
|
|
| \(F\) |
\(T\) |
\(T\) |
|
|
|
| \(F\) |
\(T\) |
\(F\) |
|
|
|
| \(F\) |
\(F\) |
\(T\) |
|
|
|
| \(F\) |
\(F\) |
\(F\) |
|
|
|
Given a truth table, how do we find an expression using the input
variables and logical operators that has the output values specified in
this table?
Application: design a circuit given a desired
input-output relationship.
| Input |
Output |
| \(p\) |
\(q\) |
\(mystery_1\) |
\(mystery_2\) |
| \(T\) |
\(T\) |
\(T\) |
\(F\) |
| \(T\) |
\(F\) |
\(T\) |
\(F\) |
| \(F\) |
\(T\) |
\(F\) |
\(F\) |
| \(F\) |
\(F\) |
\(T\) |
\(T\) |
Expressions that have output \(mystery_1\) are
Expressions that have output \(mystery_2\) are
Definition An expression built of
variables and logical operators is in disjunctive normal
form (DNF) means that it is an OR of ANDs of variables
and their negations.
Definition An expression built of
variables and logical operators is in conjunctive normal
form (CNF) means that it is an AND of ORs of variables
and their negations.
Extra example: An expression that has output ?
is:
| Input |
Output |
| \(p\) |
\(q\) |
\(r\) |
? |
| \(T\) |
\(T\) |
\(T\) |
\(T\) |
| \(T\) |
\(T\) |
\(F\) |
\(T\) |
| \(T\) |
\(F\) |
\(T\) |
\(F\) |
| \(T\) |
\(F\) |
\(F\) |
\(T\) |
| \(F\) |
\(T\) |
\(T\) |
\(F\) |
| \(F\) |
\(T\) |
\(F\) |
\(F\) |
| \(F\) |
\(F\) |
\(T\) |
\(T\) |
| \(F\) |
\(F\) |
\(F\) |
\(F\) |
Review: Week 3
Monday
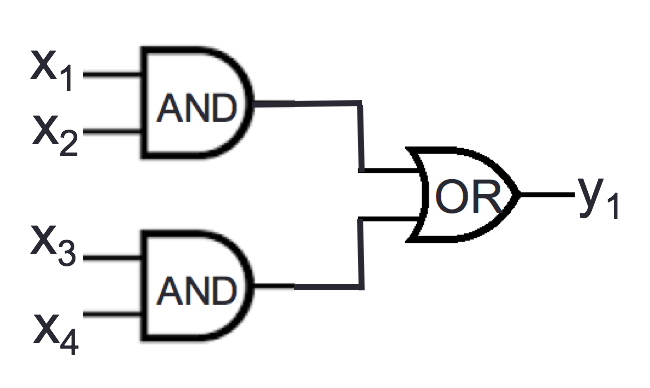
Consider the logic circuit
For which of the following settings(s) of input values is the output
\(y_1 = 0\)? (Select all and only
those that apply.)
\(x_1 = 0\), \(x_2 = 0\), \(x_3
= 0\), and \(x_4 = 0\)
\(x_1 = 1\), \(x_2 = 1\), \(x_3
= 1\), and \(x_4 = 1\)
\(x_1 = 1\), \(x_2 = 0\), \(x_3
= 0\), and \(x_4 = 1\)
\(x_1 = 0\), \(x_2 = 0\), \(x_3
= 1\), and \(x_4 = 1\)
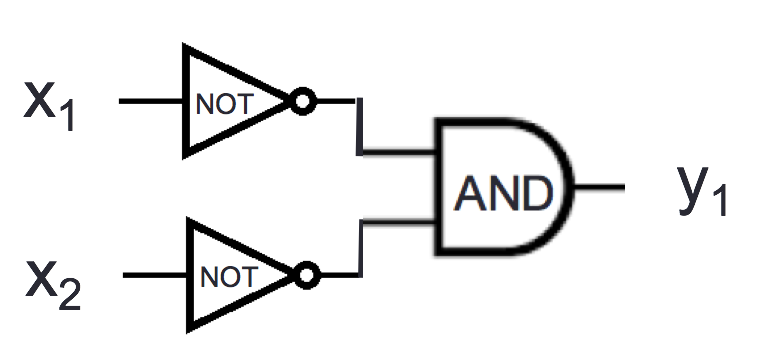
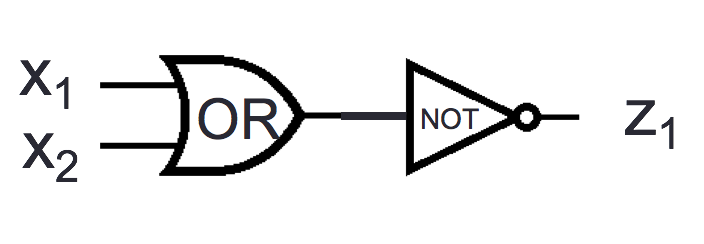
Consider the logic circuits
For which of the following settings(s) of input values do the outputs
of these circuits have the same value, i.e. \(y_1 = z_1\)? (Select all and only those
that apply.)
\(x_1 = 1\), \(x_2 = 1\)
\(x_1 = 1\), \(x_2 = 0\)
\(x_1 = 0\), \(x_2 = 1\)
\(x_1 = 0\), \(x_2 = 0\)
For each of the following compound propositions, determine if it
is in DNF, CNF, both, or neither.
\((x \lor y \lor z) \land (x \land
\lnot y \land z)\)
\(\lnot (x \land y \land z) \land \lnot
(\lnot x \land y \land \lnot z)\)
Wednesday October
13
Proposition: Declarative sentence that
is true or false (not both).
Propositional variable: Variable that
represents a proposition.
Compound proposition: New proposition
formed from existing propositions (potentially) using logical operators.
Note: A propositional variable is one example of a
compound proposition.
Truth table: Table with one row for
each of the possible combinations of truth values of the input and an
additional column that shows the truth value of the result of the
operation corresponding to a particular row.
Logical equivalence : Two compound
propositions are logically equivalent
means that they have the same truth values for all settings of truth
values to their propositional variables.
Tautology: A compound proposition that
evaluates to true for all settings of truth values to its propositional
variables; it is abbreviated \(T\).
Contradiction: A compound proposition
that evaluates to false for all settings of truth values to its
propositional variables; it is abbreviated \(F\).
Contingency: A compound proposition
that is neither a tautology nor a contradiction.
Label each of the following as a tautology, contradiction, or
contingency.
\(p \land p\)
\(p \oplus p\)
\(p \lor p\)
\(p \lor \lnot p\)
\(p \land \lnot p\)
Extra Example: Which of the compound
propositions in the table below are logically equivalent?
| Input |
Output |
| \(p\) |
\(q\) |
\(\lnot (p
\land \lnot q)\) |
\(\lnot (\lnot
p \lor \lnot q)\) |
\((\lnot p
\lor q)\) |
\((\lnot q
\lor \lnot p)\) |
\((p \land
q)\) |
| \(T\) |
\(T\) |
|
|
|
|
|
| \(T\) |
\(F\) |
|
|
|
|
|
| \(F\) |
\(T\) |
|
|
|
|
|
| \(F\) |
\(F\) |
|
|
|
|
|
| Input |
Output |
|
|
Conjunction |
Exclusive or |
Disjunction |
Conditional |
Biconditional |
| \(p\) |
\(q\) |
\(p \wedge
q\) |
\(p \oplus q\) |
\(p
\vee q\) |
\(p \to
q\) |
\(p
\leftrightarrow q\) |
| \(T\) |
\(T\) |
\(T\) |
\(F\) |
\(T\) |
\(T\) |
\(T\) |
| \(T\) |
\(F\) |
\(F\) |
\(T\) |
\(T\) |
\(F\) |
\(F\) |
| \(F\) |
\(T\) |
\(F\) |
\(T\) |
\(T\) |
\(T\) |
\(F\) |
| \(F\) |
\(F\) |
\(F\) |
\(F\) |
\(F\) |
\(T\) |
\(T\) |
|
|
“\(p\)
and \(q\)” |
“\(p\)
xor \(q\)” |
“\(p\)
or \(q\)” |
“if \(p\) then \(q\)” |
“\(p\)
if and only if \(q\)” |
The only way to make the conditional statement \(p \to q\) false is to
| The
hypothesis of \(p \to q\) is |
|
The
antecedent of \(p \to q\) is |
|
|
|
|
|
| The
conclusion of \(p \to q\) is |
|
The
consequent of \(p \to q\) is |
|
|
|
|
|
The converse of \(p \to q\) is
The inverse of \(p \to q\) is
The contrapositive of \(p \to q\) is
We can use a recursive definition to describe all compound
propositions that use propositional variables from a specified
collection. Here’s the definition for all compound propositions whose
propositional variables are in \(\{p,
q\}\).
\[\begin{array}{ll}
\textrm{Basis Step: } & p \textrm{ and } q \textrm{ are each a
compound proposition} \\
\textrm{Recursive Step: } & \textrm{If } x \textrm{ is a compound
proposition then so is } (\lnot x)
\textrm{ and if } \\
& x \textrm{ and } y \textrm{ are both compound propositions then so
is each of }\\
&(x \land y), (x \oplus y), (x \lor y), (x \to y), (x
\leftrightarrow y)
\end{array}\]
Order of operations (Precedence) for logical operators:
Negation, then conjunction / disjunction, then conditional /
biconditionals.
Example: \(\lnot p \lor \lnot q\)
means \((\lnot p) \lor (\lnot q)\).
(Some) logical equivalences
Can replace \(p\) and
\(q\) with any compound
proposition
| \(\lnot ( \lnot
p) \equiv p\) |
|
Double
negation |
|
|
|
|
|
|
| \(p \lor q
\equiv q \lor p\) |
\(p \land q
\equiv q \land p\) |
Commutativity
Ordering of terms |
|
|
|
|
|
|
| \((p \lor q)
\lor r \equiv p \lor (q \lor r)\) |
\((p \land q)
\land r \equiv p \land (q \land r)\) |
Associativity
Grouping of terms |
|
|
|
|
|
|
| \(p \land F
\equiv F\) \(p \lor T \equiv
T\) |
\(p \land T
\equiv p\) \(p \lor F \equiv
p\) |
Domination
aka short circuit evaluation |
|
|
|
|
|
|
| \(\lnot (p \land
q) \equiv \lnot p \lor \lnot q\) |
\(\lnot (p \lor
q) \equiv \lnot p \land\lnot q\) |
DeMorgan’s
Laws |
|
|
|
| \(p \to q \equiv
\lnot p \lor q\) |
|
|
|
|
|
|
|
|
| \(p \to q \equiv
\lnot q \to \lnot p\) |
|
Contrapositive |
|
|
|
|
|
|
| \(\lnot (p \to
q) \equiv p\land \lnot q\) |
|
|
|
|
|
|
|
|
| \(\lnot( p
\leftrightarrow q) \equiv p \oplus q\) |
|
|
|
|
|
|
|
|
| \(p
\leftrightarrow q \equiv q \leftrightarrow p\) |
|
|
|
|
|
Extra examples:
\(p \leftrightarrow q\) is not
logically equivalent to \(p \land q\)
because
\(p \to q\) is not logically
equivalent to \(q \to p\) because
Review: Week 3
Wednesday
For each of the following propositions, indicate exactly one
of:
There is no assignment of truth values to its variables that
makes it true,
There is exactly one assignment of truth values to its variables
that makes it true, or
There are exactly two assignments of truth values to its
variables that make it true, or
There are exactly three assignments of truth values to its
variables that make it true, or
All assignments of truth values to its variables make it
true.
\(x \land y \land (x \lor
y)\)
\(\lnot x \land y \land (x \lor
y)\)
\(x \land \lnot y \land (x \land
y)\)
\(\lnot x \land (y \lor \lnot
y)\)
\(x \land (y \lor \lnot
x)\)
For each of the following propositions, indicate exactly one
of:
There is no assignment of truth values to its variables that
makes it true,
There is exactly one assignment of truth values to its variables
that makes it true, or
There are exactly two assignments of truth values to its
variables that make it true, or
There are exactly three assignments of truth values to its
variables that make it true, or
All assignments of truth values to its variables make it
true.
\((p \leftrightarrow q) \oplus (p \land
q)\)
\((p \to q) \vee (q \to
p)\)
\((p \to q) \land (q \to
p)\)
\(\lnot (p \to q)\)
Friday October 15
Common ways to express logical operators in
English:
Negation \(\lnot p\) can be said in English as
Conjunction \(p \land q\) can be said in English as
Exclusive or \(p \oplus q\) can be said in English as
Disjunction \(p \lor q\) can be said in English as
Conditional \(p \to q\) can be said in English as
2
if \(p\), then \(q\).
\(p\) is sufficient for \(q\).
\(q\) when \(p\).
\(q\) whenever \(p\).
\(p\) implies \(q\).
\(q\) follows from \(p\).
\(p\) is sufficient for \(q\).
\(q\) is necessary for \(p\).
\(p\) only if \(q\).
Biconditional
\(p\) if and only if \(q\).
\(p\) iff \(q\).
If \(p\) then \(q\), and conversely.
\(p\) is necessary and
sufficient for \(q\).
Translation: Express each of the
following sentences as compound propositions, using the given
propositions.
2 “A sufficient condition for the warranty to be good is
that you bought the computer less than a year ago" \[\begin{aligned}
w &\text{ is ``the warranty is good"} \\
b &\text{ is ``you bought the computer less than a year ago"}
\\
\end{aligned}\]
2 “Whenever the message was sent from an unknown system,
it is scanned for viruses." \[\begin{aligned}
s &\text{ is ``The message is scanned for viruses"} \\
u &\text{ is ``The message was sent from an unknown system"}
\\
\end{aligned}\]
2 “I will complete my to-do list only if I put a
reminder in my calendar" \[\begin{aligned}
d &\text{ is ``I will complete my to-do list"} \\
c &\text{ is ``I put a reminder in my calendar"} \\
\end{aligned}\]
Definition: A collection of compound
propositions is called consistent if there
is an assignment of truth values to the propositional variables that
makes each of the compound propositions true.
Consistency:
Whenever the system software is being upgraded, users cannot access
the file system. If users can access the file system, then they can save
new files. If users cannot save new files, then the system software is
not being upgraded.
Translate to symbolic compound propositions
Look for some truth assignment to the propositional variables for
which all the compound propositions output \(T\)
Review: Week 3
Friday
Express each of the following sentences as compound propositions,
using the given propositions.
“If you try to run Zoom while your computer is running many
applications, the video is likely to be choppy and laggy." \(t\) is “you run Zoom while your computer is
running many applications”, \(c\) is
“the video is likely to be choppy”, \(g\) is “the video is likely to be
laggy”
\(t \to (c \land g)\)
\((c \land g) \to t\)
\((c \land g) \leftrightarrow
t\)
\(t \oplus (c \land
g)\)
“To connect wirelessly on campus without logging in you need to
use the UCSD-Guest network." \(c\) is
“connect wirelessly on campus”, \(g\)
is “logging in”, and \(u\) is “use
UCSD-Guest network”.
\(c \land \lnot g \land
u\)
\((c \land \lnot g) \lor
u\)
\((c \land \lnot g) \oplus
u\)
\((c \land \lnot g) \to
u\)
\(u \to (c \land \lnot
g)\)
\(u \leftrightarrow (c \land \lnot
g)\)
For each of the following system specifications, identify the
compound propositions that give their translations to logic and then
determine if the translated collection of compound propositions is
consistent.
Specification: If the computer is out of memory, then network
connectivity is unreliable. No disk errors can occur when the computer
is out of memory. Disk errors only occur when network connectivity is
unreliable.
Translation: \(M =\) “the computer
is out of memory"; \(N =\) “network
connectivity is unreliable"; \(D =\)
“disk errors can occur".
\[\begin{aligned}
&\neg M \to N \\ & \neg D \to M \\ & D \to N
\end{aligned}\]
\[\begin{aligned}
&M \to \neg N \\ & \neg D \wedge M \\ & N \to D
\end{aligned}\]
\[\begin{aligned}
&M \to N \\ & M \to \neg D \\ & \neg N \to \neg D
\end{aligned}\]
Specification: Whether you think you can, or you think you can’t
- you’re right.
Translation: \(T =\) “you think you
can"; \(C =\) “you can".
\[\begin{aligned}
&T \to C \\& \neg T \to \neg C
\end{aligned}\]
\[\begin{aligned}
&T \wedge C \\ & \neg T \wedge \neg C
\end{aligned}\]
\[\begin{aligned}
&T \to \neg T \\ & C \to \neg C
\end{aligned}\]
Specification: A secure password must be private and complicated.
If a password is complicated then it will be hard to remember. People
write down hard-to-remember passwords. If a password is written down,
it’s not private. The password is secure.
Translation: \(S =\) “the password
is secure"; \(P =\) “the password is
private"; \(C =\) “the password is
complicated"; \(H =\) “the password is
hard to remember"; \(W =\) “the
password is written down".
\[\begin{aligned}
&\neg (P \wedge C) \to \neg S \\ & C \to H \\ & W \wedge
H \\ & W \to \neg P \\ & S
\end{aligned}\]
\[\begin{aligned}
&(P \wedge C) \to S \\ & C \to H\\ & W \to H \\ &
W \to P \\ & S
\end{aligned}\]
\[\begin{aligned}
& S \to (P \wedge C) \\ & C \to H\\ & H \to W \\ &
W \to \neg P \\ & S
\end{aligned}\]