Today’s session is on Zoom, log in with your @ucsd.edu account https://ucsd.zoom.us/j/97431852722 Meeting ID: 974 3185 2722
Recall the definitions: The set of RNA strands \(S\) is defined (recursively) by: \[\begin{array}{ll} \textrm{Basis Step: } & \texttt{A}\in S, \texttt{C}\in S, \texttt{U}\in S, \texttt{G}\in S \\ \textrm{Recursive Step: } & \textrm{If } s \in S\textrm{ and }b \in B \textrm{, then }sb \in S \end{array}\] where \(sb\) is string concatenation.
The function rnalen that computes the length of RNA strands in \(S\) is defined recursively by: \[\begin{array}{llll} & & \textit{rnalen} : S & \to \mathbb{Z}^+ \\ \textrm{Basis Step:} & \textrm{If } b \in B\textrm{ then } & \textit{rnalen}(b) & = 1 \\ \textrm{Recursive Step:} & \textrm{If } s \in S\textrm{ and }b \in B\textrm{, then } & \textit{rnalen}(sb) & = 1 + \textit{rnalen}(s) \end{array}\]
The function basecount that computes the number of a given base \(b\) appearing in a RNA strand \(s\) is defined recursively by: \[\begin{array}{llll} & & \textit{basecount} : S \times B & \to \mathbb{N} \\ \textrm{Basis Step:} & \textrm{If } b_1 \in B, b_2 \in B & \textit{basecount}(~(b_1, b_2)~) & = \begin{cases} 1 & \textrm{when } b_1 = b_2 \\ 0 & \textrm{when } b_1 \neq b_2 \\ \end{cases} \\ \textrm{Recursive Step:} & \textrm{If } s \in S, b_1 \in B, b_2 \in B &\textit{basecount}(~(s b_1, b_2)~) & = \begin{cases} 1 + \textit{basecount}(~(s, b_2)~) & \textrm{when } b_1 = b_2 \\ \textit{basecount}(~(s, b_2)~) & \textrm{when } b_1 \neq b_2 \\ \end{cases} \end{array}\]
At this point, we’ve seen the proof strategies
2
A counterexample to prove that \(\forall x P(x)\) is false.
A witness to prove that \(\exists x P(x)\) is true.
Proof of universal by exhaustion to prove that \(\forall x \, P(x)\) is true when \(P\) has a finite domain
Proof by universal generalization to prove that \(\forall x \, P(x)\) is true using an arbitrary element of the domain.
To prove that \(\exists x P(x)\) is false, write the universal statement that is logically equivalent to its negation and then prove it true using universal generalization.
To prove that \(p \land q\) is true, have two subgoals: subgoal (1) prove \(p\) is true; and, subgoal (2) prove \(q\) is true. To prove that \(p \land q\) is false, it’s enough to prove that \(p\) is false. To prove that \(p \land q\) is false, it’s enough to prove that \(q\) is false.
Proof of conditional by direct proof
Proof of conditional by contrapositive proof
Proof of disjuction using equivalent conditional: To prove that the disjunction \(p \lor q\) is true, we can rewrite it equivalently as \(\lnot p \to q\) and then use direct proof or contrapositive proof.
Proof by cases.
Which proof strategies could be used to prove each of the following statements?
Hint: first translate the statements to English and identify the main logical structure.
\(\forall s \in S~(~rnalen(s) > 0~)\)
\(\forall b \in B~\exists s \in S~(~basecount(~(s,b)~)~ > 0~)\)
\(\forall s \in S ~\exists b\in B ~(~basecount(~(s,b)~) > 0~)\)
\(\exists s \in S \, (\textit{rnalen(s)} = \textit{basecount}(~(s, \texttt{A})~)\)
\(\forall s \in S \, (\textit{rnalen(s)} \geq \textit{basecount}(~(s, \texttt{A})~))\)
Claim \(\forall s \in S ~(~rnalen(s) > 0~)\)
Proof: Let \(s\) be an arbitrary RNA strand. By the recursive definition of \(S\), either \(s \in B\) or there is some strand \(s_0\) and some base \(b\) such that \(s = s_0 b\). We will show that the inequality holds for both cases.
\(\phantom{Basis}\) Case: Assume \(s \in B\). We need to show \(rnalen(s) > 0\). By the basis step in the definition of \(rnalen\), \[rnalen(s) = 1\] which is greater than \(0\), as required.
\(\phantom{Recursive}\) Case: Assume there is some strand \(s_0\) and some base \(b\) such that \(s = s_0 b\). We will show (the stronger claim) that \[\forall u \in S ~\forall b \in B ~( ~\textit{rnalen}(u) >0 \to \textit{rnalen}(ub) >0 ~)\] Consider an arbitrary RNA strand \(u\) and an arbitrary base \(b\), and assume towards a direct proof,\(~~{\phantom{ this is the induction hypothesis}}~~\) that \[rnalen(u) > 0\] We need to show that \(rnalen(ub) > 0\). \[rnalen(ub) = 1 + rnalen (u) > 1 + 0 = 1 > 0\] as required.
Claim \(\forall s \in S \, (\textit{rnalen(s)} \geq \textit{basecount}(~(s, \texttt{A})~))\):
Proof: We proceed by structural induction on the recursively defined set \(S\).
Basis Case: We need to prove that the inequality holds for each element in the basis step of the recursive definition of \(S\). Need to show \[\begin{aligned} &(~ rnalen(\texttt{A}) \geq basecount(~(\texttt{A}, \texttt{A})~)~) \land (~ rnalen(\texttt{C}) \geq basecount(~(\texttt{C}, \texttt{A})~)~) \\ \land & (~ rnalen(\texttt{U}) \geq basecount(~(\texttt{U}, \texttt{A})~)~) \land (~ rnalen(\texttt{G}) \geq basecount(~(\texttt{G}, \texttt{A})~)~) \end{aligned}\] We calculate, using the definitions of \(rnalen\) and \(basecount\):
Recursive Case: We will prove that \[\forall u \in S ~\forall b \in B ~( ~rnalen(u) \geq basecount(~(u, \texttt{A})~) \to rnalen(ub) \geq basecount(~(ub, \texttt{A})~)\]
Consider arbitrary RNA strand \(u\) and arbitrary base \(b\). Assume, as the induction hypothesis, that \(rnalen(u) \geq basecount(~(u,\texttt{A})~)\). We need to show that \(rnalen(ub) \geq basecount(~(ub, \texttt{A})~)\).
Using the recursive step in the definition of the function \(rnalen\): \[rnalen(ub) = 1 + rnalen(u)\] The recursive step in the definition of the function \(basecount\) has two cases. We notice that \(b = \texttt{A}\lor b \neq \texttt{A}\) and we proceed by cases.
Case i. Assume \(b = \texttt{A}\).
Using the first case in the recursive step in the definition of the function \(basecount\): \[basecount(~(ub, \texttt{A})~) = 1 + basecount(~(u,\texttt{A})~)\] By the induction hypothesis, we know that \(basecount(~(u,\texttt{A})~) \leq rnalen(u)\) so: \[basecount(~(ub, \texttt{A})~) = 1 + basecount(~(u,\texttt{A})~) \leq 1 + rnalen(u) = rnalen (ub)\] and, thus, \(basecount(~(ub,\texttt{A})~) \leq rnalen(ub)\), as required.
Case ii. Assume \(b \neq \texttt{A}\).
Using the second case in the recursive step in the definition of the function \(basecount\): \[basecount(~(ub, \texttt{A})~) = basecount(~(u,\texttt{A})~)\] By the induction hypothesis, we know that \(basecount(~(u,\texttt{A})~) \leq rnalen(u)\) so: \[basecount(~(ub, \texttt{A})~) = basecount(~(u,\texttt{A})~) \leq rnalen(u) < 1 + rnalen(u) = rnalen (ub)\] and, thus, \(basecount(~(ub,\texttt{A})~) \leq rnalen(ub)\), as required.
Recall the definitions of the functions \(rnalen\) and \(basecount\) from class.
Select all and only options that give a witness for the existential quantification \[\exists s \in S ~(~rnalen(s) = basecount(~(s,\texttt{U})~)~)\]
\(\texttt{A}\)
\(\texttt{U}\texttt{U}\)
\(\texttt{C}\texttt{U}\)
\((\texttt{U}, 1)\)
None of the above.
Select all and only options that give a counterexample for the universal quantification \[\forall s \in S ~(~rnalen(s) > basecount(~(s,\texttt{G})~)~)\]
\(\texttt{U}\)
\(\texttt{G}\texttt{G}\)
\(\texttt{A}\texttt{G}\)
\(\texttt{C}\texttt{U}\texttt{G}\)
None of the above.
Select all and only the true statements
\(\forall s \in S ~\exists b \in B ~\left(~rnalen(s) = basecount(~(s,b)~)~ \right)\)
\(\exists s \in S ~\forall b \in B ~\left(~rnalen(s) = basecount(~(s,b)~)~ \right)\)
\[\begin{aligned} \forall s_1 \in S~\forall s_2 \in S ~&\forall b \in B ~\big( ~\big( rnalen(s_1) = basecount(~(s_1,b)~) \\ &\land rnalen(s_2) = basecount(~(s_2,b)~) \land rnalen(s_1) = rnalen(s_2) \big) \to s_1 = s_2 \big) \end{aligned}\]
None of the above.
To organize our proofs, it’s useful to highlight which claims are most important for our overall goals. We use some terminology to describe different roles statements can have.
Theorem: Statement that can be shown to be true, usually an important one.
Less important theorems can be called proposition, fact, result, claim.
Lemma: A less important theorem that is useful in proving a theorem.
Corollary: A theorem that can be proved directly after another one has been proved, without needing a lot of extra work.
Invariant: A theorem that describes a property that is true about an algorithm or system no matter what inputs are used.

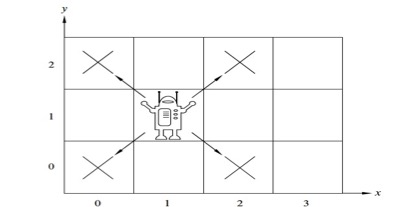
Theorem: A robot on an infinite 2-dimensional integer grid starts at \((0,0)\) and at each step moves to diagonally adjacent grid point. This robot can / cannot (circle one) reach \((1,0)\).
Definition The set of positions the robot can visit \(P\) is defined by: \[\begin{array}{ll} \textrm{Basis Step: } & (0,0) \in P \\ \textrm{Recursive Step: } & \textrm{If } (x,y) \in P \textrm{, then } \phantom{(x+1, y+1), (x+1, y-1), (x-1, y-1), (x-1, y+1)} \textrm{ are also in } P \end{array}\]
Example elements of \(P\) are:
Lemma: \(\forall (x,y) \in P( x+y \textrm{ is an even integer}~)\)
Why are we calling this a lemma?
Proof of theorem using lemma: To show is \((1,0) \notin P\). Rewriting the lemma to explicitly restrict the domain of the universal, we have \(\forall (x,y) ~(~ (x,y) \in P \to (x+y \textrm{ is an even integer})~)\). Since the universal is true, \((~ (1,0) \in P \to (1+0 \textrm{ is an even integer})~)\) is a true statement. Evaluating the conclusion of this conditional statement: By definition of long division, since \(1 = 0 \cdot 2 + 1\) (where \(0 \in \mathbb{Z}\) and \(1 \in \mathbb{Z}\) and \(0 \leq 1 < 2\) mean that \(0\) is the quotient and \(1\) is the remainder), \(1 ~\textrm{\bf mod}~ 2 = 1\) which is not \(0\) so the conclusion is false. A true conditional with a false conclusion must have a false hypothesis. Thus, \((1,0) \notin P\), QED. \(\square\)
Proof of lemma by structural induction:
Basis Step:
Recursive Step: Consider arbitrary \((x,y) \in P\). To show is: \[(x+y \text{ is an even integer}) \to (\text{sum of coordinates of next position is even integer})\] Assume as the induction hypothesis, IH that:
The set \(\mathbb{N}\) is recursively defined. Therefore, the function \(sumPow: \mathbb{N} \to \mathbb{N}\) which computes, for input \(i\), the sum of the nonnegative powers of \(2\) up to and including exponent \(i\) is defined recursively by
\[\begin{aligned} {2} \text{Basis step: } \qquad & sumPow(0) = 1 &\\ \text{Recursive step: } & \text{If } x \in \mathbb{N} \text{, then } &sumPow(x+1) = sumPow(x) + 2^{x+1} \end{aligned}\]
\(sumPow(0) =\)
\(sumPow(1) =\)
\(sumPow(2) =\)
Fill in the blanks in the following proof of \[\forall n \in \mathbb{N}~(sumPow(n) = 2^{n+1} - 1)\]
Proof: Since \(\mathbb{N}\) is recursively defined, we proceed by .
Basis case: We need to show that . Evaluating each side: \(LHS = sumPow(0) = 1\) by the basis case in the recursive definition of \(sumPow\); \(RHS = 2^{0+1} - 1 = 2^1 - 1 = 2-1 = 1\). Since \(1=1\), the equality holds.
Recursive case: Consider arbitrary natural number \(n\) and assume, as the that \(sumPow(n) = 2^{n+1} - 1\). We need to show that . Evaluating each side: \[LHS = sumPow(n+1) \overset{\text{rec def}}{=} sumPow(n) + 2^{n+1}\overset{\text{IH}}{=} (2^{n+1} - 1) + 2^{n+1}.\] \[RHS = 2^{(n+1)+1}- 1 \overset{\text{exponent rules}}{=} 2 \cdot 2^{n+1} -1 = \left(2^{n+1} + 2^{n+1} \right) - 1 \overset{\text{regrouping}}{=} (2^{n+1} - 1) + 2^{n+1}\] Thus, \(LHS = RHS\). The structural induction is complete and we have proved the universal generalization. \(\square\)
Recall the set \(P\) defined by the recursive definition \[\begin{array}{ll} \textrm{Basis Step: } & (0,0) \in P\\ \textrm{Recursive Step: } & \textrm{If } (x,y) \in P \textrm{ then } (x+1, y+1) \in P \textrm{ and } (x+1, y-1) \in P \textrm{ and }\\ & (x-1,y-1) \in P \textrm{ and } (x-1, y+1) \in P \end{array}\]
Select all and only the ordered pairs below that are elements of \(P\)
\((0,0)\)
\((4,0)\)
\((1,1)\)
\((1.5,2.5)\)
\((0, -2)\)
What is another description of the set \(P\) ? (Select all and only the true descriptions.)
\(\mathbb{Z} \times \mathbb{Z}\)
\(\{ (n,n) ~|~ n \in \mathbb{Z} \}\)
\(\{ (a,b) \in \mathbb{Z} \times \mathbb{Z} ~|~ (a+b) \textbf{ mod } 2 =0 \}\)
Select all and only the true statements below about the relationship between structural induction and mathematical induction.
Both structural induction and mathematical induction are proof strategies that may be useful when proving universal claims about recursively defined sets.
Mathematical induction is a special case of structural induction, for the case when the domain of quantification is \(\{ n \in \mathbb{Z} \mid n \geq b\}\) for some integer \(b\).
Universal claims about the set of all integers may be proved using structural induction but not using mathematical induction.
Consider the following function definitions \[2^n: \mathbb{N} \to \mathbb{N} \text{ given by } 2^0 = 1 ~~\text{ and }~~ 2^{n+1} = 2 \cdot 2^n\] \[n!: \mathbb{N} \to \mathbb{N} \text{ given by } 0! = 1 ~~\text{ and }~~ (n+1)! = (n+1) n!\]
Select all and only true statements below:
\(2^0 < 0!\)
\(2^1 < 1!\)
\(2^2 < 2!\)
\(2^3 < 3!\)
\(2^4 < 4!\)
\(2^5 < 5!\)
\(2^6 < 6!\)
\(2^7 < 7!\)
Fill in the blanks in the following proof.
Claim: For all integers \(n\) greater than or equal to \(4\), \(2^n <
n!\)
Proof: We proceed by mathematical
induction on the set of integers greater than or equal to \(4\).
Basis step: Using the BLANK 1,
\[2^4 = 2 \cdot 2^3 = 2 \cdot 2 \cdot 2^2 = 2
\cdot 2 \cdot 2 \cdot 2^1 =
2 \cdot 2 \cdot 2 \cdot 2 \cdot 2^0 =
2 \cdot 2 \cdot 2 \cdot 2 \cdot 1 = 16\] and \[4! = 4 \cdot 3! = 4 \cdot 3 \cdot 2!
= 4 \cdot 3 \cdot 2 \cdot 1! = 4 \cdot 3 \cdot 2 \cdot 1 \cdot 0!
= 4 \cdot 3 \cdot 2 \cdot 1 \cdot 1 = 24\] Since \(16 < 24\), we have proved that \(2^4 < 4!\) , as required.
Recursive step: Consider an arbitrary
integer \(k\) that is greater than or
equal to \(4\) and assume as the
BLANK 2, that \(2^k < k!\) .
We want to show that \(2^{k+1} <
(k+1)!\) . \[\begin{aligned}
2^{k+1} &= 2 \cdot 2^{k} \qquad \text{by
}\underline{\hspace{0.2in}BLANK 3\hspace{0.2in}}\\
&< 2 \cdot k! \qquad \text{by
}\underline{\hspace{0.2in}BLANK 4\hspace{0.2in}}\\
&< k \cdot k! \qquad \text{by
}\underline{\hspace{0.2in}BLANK 5\hspace{0.2in}}\\
&< (k+1) \cdot k! \qquad \text{by
}\underline{\hspace{0.2in}BLANK 6\hspace{0.2in}}\\
&= (k+1)! \qquad \text{by }\underline{\hspace{0.2in}BLANK
7\hspace{0.2in}}\\
\end{aligned}\] as required.
properties of addition, multiplication, and \(<\) for real numbers
definitions of the functions \(2^n\) and \(n!\)
definition of \(k\)
induction hypothesis
Definition The set of linked lists of natural numbers \(L\) is defined recursively by \[\begin{array}{ll} \textrm{Basis Step: } & [] \in L \\ \textrm{Recursive Step: } & \textrm{If } l \in L\textrm{ and }n \in \mathbb{N} \textrm{, then } (n, l) \in L \end{array}\]
Visually:
Example: the list with two nodes whose first node has \(20\) and whose second node has \(42\)
Definition: The length of a linked list of natural numbers \(L\), \(length: L \to \mathbb{N}\) is defined by \[\begin{array}{llll} \textrm{Basis Step:} & & length(~[]~) &= 0 \\ \textrm{Recursive Step:} & \textrm{If } l \in L\textrm{ and }n \in \mathbb{N}\textrm{, then } & length(~(n, l)~) &= 1+ length(l) \end{array}\]
Definition: The function \(prepend : L \times \mathbb{N} \to L\) that adds an element at the front of a linked list is defined by \[\phantom{prepend(~(l, n)~) = (n, l)}\]
Definition The function \(append : L \times \mathbb{N} \to L\) that adds an element at the end of a linked list is defined by \[\begin{array}{llll} \textrm{Basis Step:} & \textrm{If } m \in \mathbb{N}\textrm{ then } & \phantom{append(~([], m)~)} & \phantom{= (m, []) }\\ \textrm{Recursive Step:} & \textrm{If } l \in L\textrm{ and }n \in \mathbb{N}\textrm{ and }m \in \mathbb{N}\textrm{, then } & \phantom{append(~(~(n, l), m~)~) } &\phantom{= (n, append(~(l, m)~)~)} \end{array}\]
Claim: \(\forall l \in L ~ (~length(~append(~(l, 100)~)~) > length(l)~)\)
Proof: By structural induction on \(L\), we have two cases:
Basis Step
| 1. To Show \(length(~append(~([], 100)~)~) > length(~[]~)\) | Because \([]\) is the only element defined in the basis step of \(L\), we only need to prove that the property holds for \([]\). |
| 2. To Show \(length(~(100,[])~) > length(~[]~)\) | By basis step in definition of \(append\). |
| 3. To Show \((1 +length(~[]~)) > length(~[]~)\) | By recursive step in definition of \(length\). |
| 4. To Show \(1+0 > 0\) | By basis step in definition of \(length\). |
| 5. \(T\) | By properties of integers |
| QED | Because we got to \(T\) only by rewriting To Show to equivalent statements, using well-defined proof techniques, and applying definitions. |
Recursive Step
Consider an arbitrary: \(l' \in L\), \(n \in \mathbb{N}\), and we assume as the induction hypothesis that: \[length(~append(~(l', 100~)~)~) > length(l')\] Our goal is to show that \(length(~append( ~(~(n,l'), 100~)~)~) > length(~(n,l')~)\) is also true. We start by working with one side of the candidate inequality: \[\begin{aligned} LHS &= length(~append( ~(~ (n,l'), 100~)~)~) \\ &= length(~(n, append(~(l', 100)~)~ )~) \qquad \text{by the recursive definition of $append$}\\ &= 1 + length(~ append(~(l', 100)~) ~) \qquad \text{by the recursive definition of $length$}\\ &> 1+ length(l') \qquad \text{by the induction hypothesis}\\ &= length( (n,l') ) \qquad \text{by the recursive definition of $length$}\\ &= RHS \end{aligned}\]
Prove or disprove: \(\forall n \in \mathbb{N} ~\exists l \in L ~(~length(l) = n~)\)
Recall the definition of linked lists from class.
Consider this (incomplete) definition:
Definition The function \(\textit{increment} : \underline{\hspace{6em}}\) that adds 1 to the data in each node of a linked list is defined by: \[\begin{array}{llll} & & \textit{increment} : \underline{\hspace{3em}} & \to \underline{\hspace{3em}} \\ \textrm{Basis Step:} & & \textit{increment}([]) & = [] \\ \textrm{Recursive Step:} & \textrm{If } l \in L, n \in \mathbb{N} & \textit{increment}((n, l)) & = (1 + n, \textit{increment}(l)) \end{array}\]
Consider this (incomplete) definition:
Definition The function \(\textit{sum} : L \to \mathbb{N}\) that adds together all the data in nodes of the list is defined by: \[\begin{array}{llll} & & \textit{sum} : L & \to \mathbb{N} \\ \textrm{Basis Step:} & & \textit{sum}([]) & = 0 \\ \textrm{Recursive Step:} & \textrm{If } l \in L, n \in \mathbb{N} & \textit{sum}((n, l)) & = \underline{\hspace{8em}} \end{array}\]
You will compute a sample function application and then fill in the blanks for the domain and codomain of each of these functions.
Based on the definition, what is the result of \(\textit{increment}((4, (2, (7, []))))\)? Write your answer directly with no spaces.
Which of the following describes the domain and codomain of increment?
2
The domain is \(L\) and the codomain is \(\mathbb{N}\)
The domain is \(L\) and the codomain is \(\mathbb{N} \times L\)
The domain is \(L \times \mathbb{N}\) and the codomain is \(L\)
The domain is \(L \times \mathbb{N}\) and the codomain is \(\mathbb{N}\)
The domain is \(L\) and the codomain is \(L\)
None of the above
Assuming we would like \(sum((5, (6, [])))\) to evaluate to \(11\) and \(sum((3, (1, (8, []))))\) to evaluate to \(12\), which of the following could be used to fill in the definition of the recursive case of sum?
2
\(\begin{cases} 1 + \textit{sum}(l) & \textrm{when } n \neq 0 \\ \textit{sum}(l) & \textrm{when } n = 0 \\ \end{cases}\)
\(1 + \textit{sum}(l)\)
\(n + \textit{increment}(l)\)
\(n + \textit{sum}(l)\)
None of the above
Choose only and all of the following statements that are well-defined; that is, they correctly reflect the domains and codomains of the functions and quantifiers, and respect the notational conventions we use in this class. Note that a well-defined statement may be true or false.
2
\(\forall l \in L \, (\textit{sum}(l))\)
\(\exists l \in L \, (\textit{sum}(l) \land \textit{length}(l))\)
\(\forall l \in L \, (\textit{sum}(\textit{increment}(l)) = 10)\)
\(\exists l \in L \, (\textit{sum}(\textit{increment}(l)) = 10)\)
\(\forall l \in L \, \forall n \in \mathbb{N} \, ((n \times l) \subseteq L)\)
\(\forall l_1 \in L \, \exists l_2 \in L \, (\textit{increment}(\textit{sum}(l_1)) = l_2)\)
\(\forall l \in L \, (\textit{length}(\textit{increment}(l)) = \textit{length}(l))\)
Choose only and all of the statements in the previous part that are both well-defined and true.